Altın oran, matematik ve sanatta, bir bütünün parçaları arasında gözlemlenen, uyum açısından en yetkin boyutları verdiği sanılan geometrik ve sayısal bir oran bağıntısıdır.Eski Mısırlılar ve Yunanlar tarafından keşfedilmiş, mimaride ve sanatta kullanılmıştır.
Bir doğru parçasının |AB| Altın Oran'a uygun biçimde iki parçaya bölünmesi gerektiğinde, bu doğru öyle bir noktadan (C) bölünmelidir ki; küçük parçanın |AC| büyük parçaya |CB| oranı, büyük parçanın |CB| bütün doğruya |AB| oranına eşit olsun.
Altın Oran, pi (π) gibi irrasyonel bir sayıdır ve ondalık sistemde yazılışı; 1,618033988749894...'tür. -noktadan sonraki ilk 15 basamak- Bu oranın kısaca gösterimi: 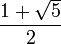 olur. Altın Oranın ifade edilmesi için kullanılan sembol, Fi yani Φ'dir.
olur. Altın Oranın ifade edilmesi için kullanılan sembol, Fi yani Φ'dir.
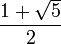 olur. Altın Oranın ifade edilmesi için kullanılan sembol, Fi yani Φ'dir.
olur. Altın Oranın ifade edilmesi için kullanılan sembol, Fi yani Φ'dir.
Altın Oran, matematikte ve fiziksel evrende ezelden beri var olmasına rağmen, insanlar tarafından ne zaman keşfedildiğine ve kullanılmaya başlandığına dair kesin bir bilgi mevcut değildir. Tarih boyunca birçok defa yeniden keşfedilmiş olma olasılığı kuvvetlidir.
Altın Oran'ın Latince karşılığını ilk kullanan muhtemelen Leonardo da Vinci 'dir. Rönesans sanatçıları Altın Oran'ı tablolarında ve heykellerinde denge ve güzelliği elde etmek amacıyla sıklıkla kullanmışlardır. Örneğin Leonardo da Vinci, Son Yemek adlı tablosunda, İsa'nın ve havarilerin oturduğu masanın boyutlarından, arkadaki duvar ve pencerelere kadar Altın Oran'ı uygulamıştır.
Altın Oran, bir sayının insanlık, bilim ve sanat tarihinde oynadığı inanılmaz bir roldür. Phi, evren ve yaşamı anlama konusunda bizlere yeni kapılar açmaya devam etmektedir. 1970'lerde Roger Penrose, o güne kadar imkânsız olduğu düşünülen, "yüzeylerin beşli simetri ile katlanması"nı Altın Oran sayesinde bulmuştur.
Mısırlılar tarafından Piramitlerin yapımında kullanıldığı düşünülen altın orandaha sonraları Yunanlılar tarafından Antik Dönem heykellerinin yapımında kullanılmıştır. Keops Piramidi incelendiğinde zeminde yer alan kare büyüklüğünde bir daire çizildiğinde bu dairenin piramidin yandan bakıldığında oluşan üçgen ile aynı büyüklükte olduğu farkedilecektir.
Bunların dışında özellikle yüzdeki dengeli görüntüyü oluşturan detaylarda da altın oranmevcuttur. Örneğin; Dudak çizgisinin bittiği noktalarla göz bebekleri aynı çizgiden geçtiğinde ve oluşan bu karenin tam ortasında burun ucu yer aldığında bu durum estetik açıdan dengeli bir görüntüyü ve altın oranı ifade eder. Aynı şekilde insan vücusunun çeşitli bölgelerinde de yine bu orana benzer oranlar bulunmaktadır. Parmak boğumlarında, el ve kollarda, bacaklarda, baş ve omuz kısmında altın oranlar söz konusudur.
Ayrıca uzay boşluğunda, DNA'da, papatya, eğrelti otu gibi bitkilerde, salyangoz, tavşan gibi havyanlarda da altın oranı yansıtan detaylar mevcuttur. Doğanın güzellik ve estetik ölçütü olarak bilinen bu oran hayvan kabuklarında, mikrobik canlılar da dahi görülürken doğada çeşitli canlılarda ve alanlarda rastlanan spiral şekli insanlar tarafından çok farklı amaçlar için kullanılabilmektedir. Örneğin; altın orana uygun bir spiral şeklinin merkezi fotoğrafçılıkta merceğin asıl merkezi olarak kabul edilmektedir. Altın oran endüstriyel tasarım açısından da önemli bir değerdir. Ev gereçlerinden, otomotiv sektörüne kadar pek çok farklı alanda modern bir görünüm elde etmek için kullanılan kıvrım ve eğimler için bu orandan yararlanılır.
Keşfedildiği dönemlerden itibaren sırasıyla mimari, sanat, matematik ve geometri, tıp, farklı bilim dalları, inançlar ve daha pek çok alanda kullanılan, yararlanılan altın oran günümüzde de değerini yitirmemiş, hala bir çok alanda faydalanılan "ilahi oran" olarak da tanımlanan bir değerdir.
Son olarak aşağıdaki video ile özetleyebiliriz:




Çok beğendim hocam güzel bir paylaşım olmuş özellikle sonundaki video ya bayıldım.Tebrik ederim.
YanıtlaSilIyisinin iyisi bu kadar iyi yapmana gerek yok çok beğendim
YanıtlaSilBu yorum bir blog yöneticisi tarafından silindi.
YanıtlaSil24 ayar değerinde altın oran konusu olmuş eline sağlık :)
YanıtlaSilBu yorum yazar tarafından silindi.
YanıtlaSilBu yorum bir blog yöneticisi tarafından silindi.
YanıtlaSilAltın oranı hep merak ederdim çok net anladım bilginiz için teşekkürler :)
YanıtlaSiliçeriği çok güzel ve açıklayıcı olmuş.paylaşımınız için teşekkürler :) :)
YanıtlaSil